Introduction
The enigmatic world of options trading has long fascinated investors seeking to harness the potential of financial markets. In this intricate realm, the mathematics of options play a crucial role in deciphering the complexities of these versatile financial instruments. Let us embark on a journey to unravel the mathematical foundations that govern options trading, empowering you to navigate this dynamic and potentially lucrative landscape.
Image: www.mdpi.com
The Genesis: Understanding Options
Options, often referred to as financial derivatives, grant the holder the right, but not the obligation, to buy (call option) or sell (put option) an underlying asset at a predefined price within a specified period. These contracts enable investors to speculate on the future direction of asset prices without incurring the obligation of ownership. The underlying asset can encompass stocks, bonds, currencies, commodities, or even indices.
The Black-Scholes Model: Unveiling Option Pricing
The Black-Scholes model, developed by Fischer Black and Myron Scholes in 1973, revolutionized the valuation of options. This mathematical formula considers various factors, including the underlying asset’s price, strike price (the predetermined price), time to expiration, risk-free interest rate, and volatility, to determine the theoretical price of an option. The model has become the industry standard for options pricing and has played a pivotal role in shaping modern trading strategies.
Greeks: The Parameters that Define
Associated with every option are Greek letters that measure the sensitivity of the option’s price to changes in various underlying factors: Delta gauges the impact of the underlying asset’s price movement; Gamma assesses the responsiveness of delta to changes in the underlying asset’s price; Theta measures the decay in option value as time passes; Rho tracks the impact of interest rate fluctuations; and Vega reflects the sensitivity of an option’s price to changes in volatility. Understanding these Greeks is crucial for managing risk and optimizing trading decisions.
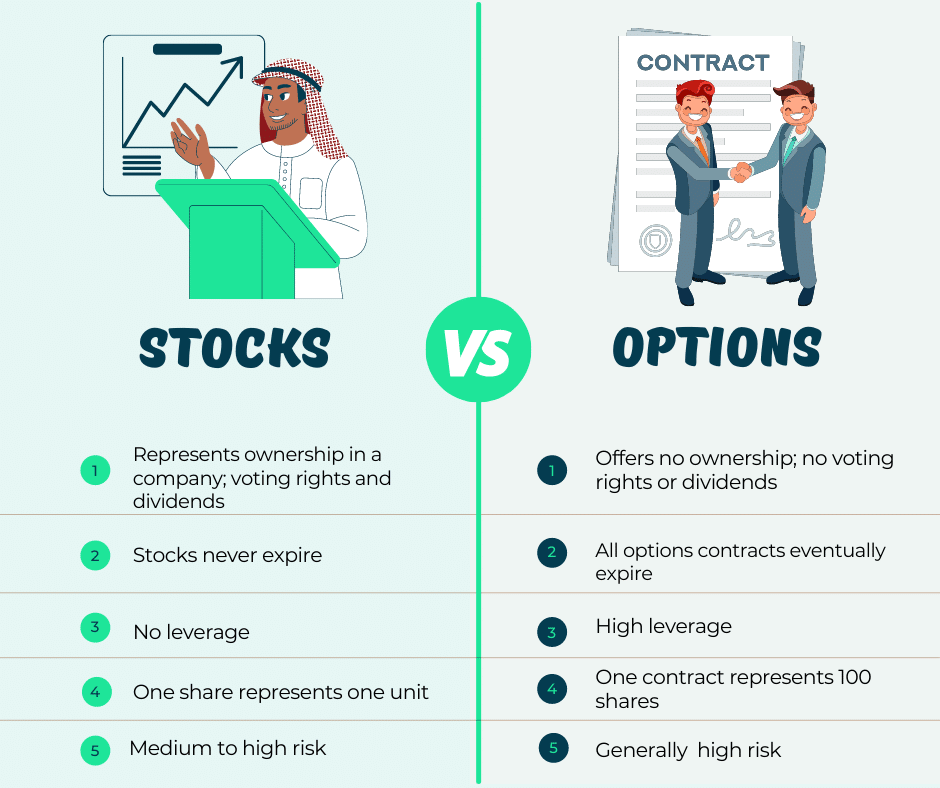
Image: www.projectfinance.com
Implied Volatility: Gauging Future Uncertainty
Implied volatility, a key input in the Black-Scholes model, reflects market participants’ expectations regarding the future volatility of the underlying asset. High implied volatility indicates that the market anticipates significant price fluctuations, while low implied volatility suggests expectations of more stable prices. Investors can use implied volatility to gauge market sentiment and adjust their trading strategies accordingly.
Strategy Applications: Navigating the Market
The mathematics of options trading extend beyond pricing formulas, empowering investors with a wide array of trading strategies. Covered calls generate income by selling covered call options, while protective puts hedge against potential downside risks. Iron condors combine multiple call and put options to create more complex strategies. Understanding the mathematical principles underlying these strategies is essential for successful implementation.
Expert Insights: Harnessing the Collective Wisdom
To delve deeper into the intricacies of options trading, it is invaluable to seek guidance from experienced professionals. Seasoned traders, financial analysts, and market experts provide invaluable insights into market dynamics, trading techniques, and risk management practices. Their knowledge and perspectives can refine your trading approach, enhancing your chances of success.
The Mathematics Of Options Trading
Conclusion
The mathematics of options trading provide a solid foundation for unraveling the complexities of these powerful financial instruments. By mastering the concepts of option pricing, the Greeks, implied volatility, and various trading strategies, investors can navigate the dynamic market landscape with greater confidence and profitability. Embark on this mathematical journey to unlock the secrets of options trading, empowering you to make informed decisions and conquer the financial markets.






