Introduction:
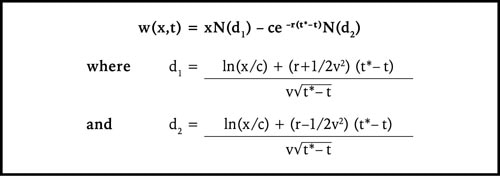
Image: oggsync.com
On the bustling floors of trading pits in the 1970s, a young economist named Fischer Black made a pivotal contribution that would forever alter the landscape of financial markets. In collaboration with Myron Scholes, a brilliant mathematician, Black developed the groundbreaking Black-Scholes option pricing model. This revolutionary formula ushered in a new era of options trading, granting traders unprecedented precision in valuing and managing option contracts.
The Dawn of Black-Scholes:
The concept of options, financial instruments that grant the buyer the right (but not obligation) to buy or sell an underlying asset at a predetermined price, had existed for centuries. However, prior to Black-Scholes, traders grappled with unreliable and subjective valuation methods. The model introduced a scientific approach, providing a mathematical framework to quantify the fair price of an option.
Key Concepts and Assumptions:
At its core, the Black-Scholes model assumes that the underlying asset’s price follows a random walk with a constant volatility. It also assumes that trading occurs continuously and that short selling and borrowing are allowed. These assumptions enable the model to calculate an option’s value based on five key factors:
- Underlying asset price
- Option strike price
- Time to expiration
- Risk-free interest rate
- Volatility
Real-World Applications:
The Black-Scholes model has myriad applications in the financial industry, including:
- Option pricing: Determining the “fair price” of options, ensuring that traders and investors pay a reasonable premium for the contract.
- Hedge fund management: Building sophisticated option strategies to hedge against risk and enhance returns.
- Trading strategies: Developing intricate trading algorithms that leverage the model’s pricing capabilities to exploit market inefficiencies.
- Valuations: Assigning fair values to companies with complex capital structures or growth potential by incorporating option-like characteristics into their valuation.
The 100,000 Trade Experiment:
In 1993, NASDAQ, in collaboration with the Chicago Board Options Exchange (CBOE), launched the “100,000 Trade Challenge” to rigorously test the accuracy of the Black-Scholes model. Over the course of a year, thousands of traders executed 100,000 equity option trades at various market conditions. The experiment revealed that on average, Black-Scholes mispriced options by just 4.4%, a remarkable validation of its predictive power.
Legacy and Limitations:
The Black-Scholes model revolutionized option trading and established itself as an industry standard. However, it has certain limitations:
- Assumption of constant volatility: Volatility often fluctuates in practice, leading to potential pricing inaccuracies.
- Simplification of market dynamics: The model does not fully account for supply and demand dynamics in thinly-traded markets.
- Lack of path dependency: Real options may have path dependency (i.e., their value depends on future price trajectory), which the model does not capture.
Conclusion:
The Black-Scholes model’s influence on financial markets cannot be overstated. Its introduction marked a paradigm shift in option pricing and sparked an explosion of derivatives markets. While it has limitations, the model remains a foundational tool for traders and investors, providing a reliable framework for understanding option valuations. Its legacy has endured the test of time, cementing Black-Scholes as one of the greatest innovations in modern finance.
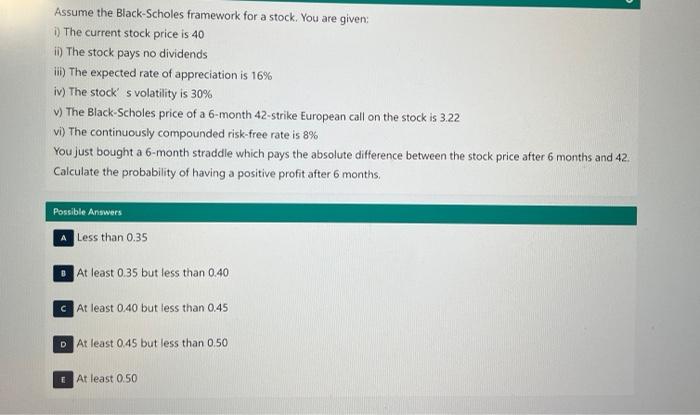
Image: www.chegg.com
Black Scholes Option Trading History 100 000
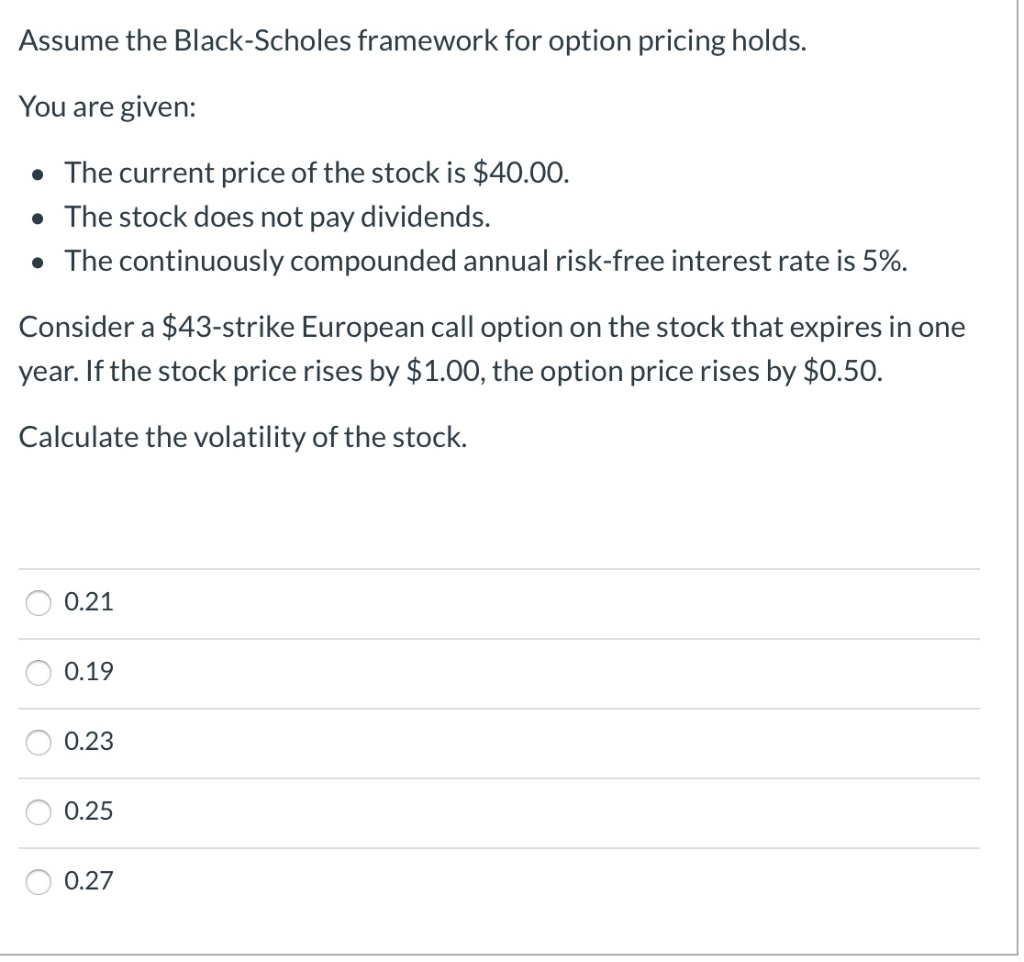
Image: www.chegg.com






