In the dynamic realm of finance, options trading stands as a captivating blend of calculated risk and strategic maneuverings. However, mastering the intricacies of this financial instrument requires a deep understanding of the underlying mathematics. Enter this comprehensive guide, where we embark on a journey to decipher the mathematical underpinnings of options trading, arming you with the knowledge to navigate the markets with confidence.

Image: hotmart.com
Options, in essence, represent the power to exercise certain financial rights at a predetermined price within a specified timeframe. These contracts between buyers and sellers confer the ability to buy or sell an underlying asset on a future date. The mathematical foundations of options pricing and valuation are instrumental in understanding their behavior and reaping their benefits.
Navigating the Black-Scholes Model: A Cornerstone of Options Pricing
As we delve into the mathematical realm of options, one model emerges as the cornerstone: the Black-Scholes model. Named after its creators, Fischer Black and Myron Scholes, this mathematical formula provides a framework for pricing European options (those exercised only at their expiration date).
At its core, the Black-Scholes model considers factors such as the current underlying asset price, strike price, time to expiration, risk-free interest rate, and volatility to determine an option’s theoretical price. By precisely calculating these parameters, traders can make informed decisions about whether to buy or sell options, as well as which strategies to employ in the quest for profit.
Greeks: Unraveling the Dynamics of Option Values
The Greek letters play a prominent role in the mathematics of options trading, offering invaluable insights into how option prices change in response to various factors. These Greek letters, including Delta, Gamma, Theta, Vega, and Rho, serve as a shorthand for calculating an option’s sensitivity to changes in variables like underlying asset price, time remaining, interest rates, and volatility.
Understanding Greek values empowers traders with the ability to determine how an option’s price will fluctuate based on different market conditions. This knowledge is indispensable for risk management, portfolio optimization, and making informed trading decisions.
Real-World Applications in Options Trading
The mathematical underpinnings of options trading provide a solid framework for making strategic decisions in the financial markets. Traders employ options to exploit various opportunities, such as:
-
Generating income: Selling premium by writing covered calls or put options can create a steady stream of income.
-
Hedging against risk: Using options to mitigate potential losses on existing investments or portfolios is a common risk management strategy.
-
Speculative trading: Capitalizing on market fluctuations by predicting the direction of an underlying asset’s price is a typical approach in options speculation.
Conclusion: Empowering Traders through Mathematical Prowess
The mathematical foundations of options trading are not merely abstract equations but rather a fundamental tool for understanding and exploiting these powerful financial instruments. By comprehending the complexities of options pricing and valuation, traders gain a competitive edge in navigating the financial markets.
To enhance your understanding even further, consider downloading an authoritative PDF resource on the mathematics of options trading. It will provide comprehensive insights into the sophisticated mathematical models and techniques that underpin this dynamic field. Embrace the journey of mathematical exploration, and unlock the potential for success in the world of options trading.
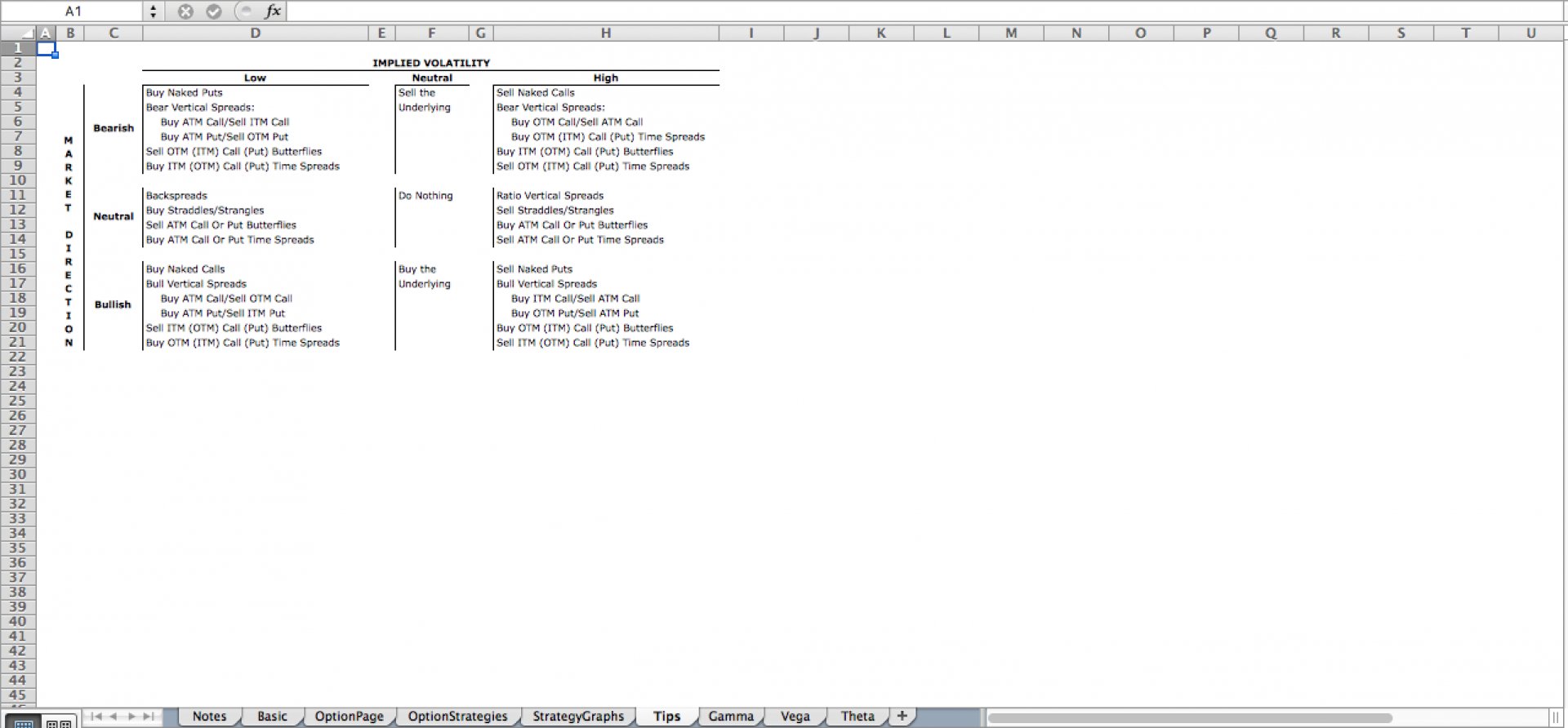
Image: www.eloquens.com
Mathematics Of Options Trading Pdf Download

Image: axel-chapter.blogspot.com






