In the fast-paced world of finance, options trading has emerged as a sophisticated investment strategy that offers traders the potential for high returns. However, mastering the intricacies of options trading requires a solid understanding of the underlying mathematics. This article delves into the key mathematical principles behind options trading, providing a comprehensive guide to help you navigate this complex financial instrument.
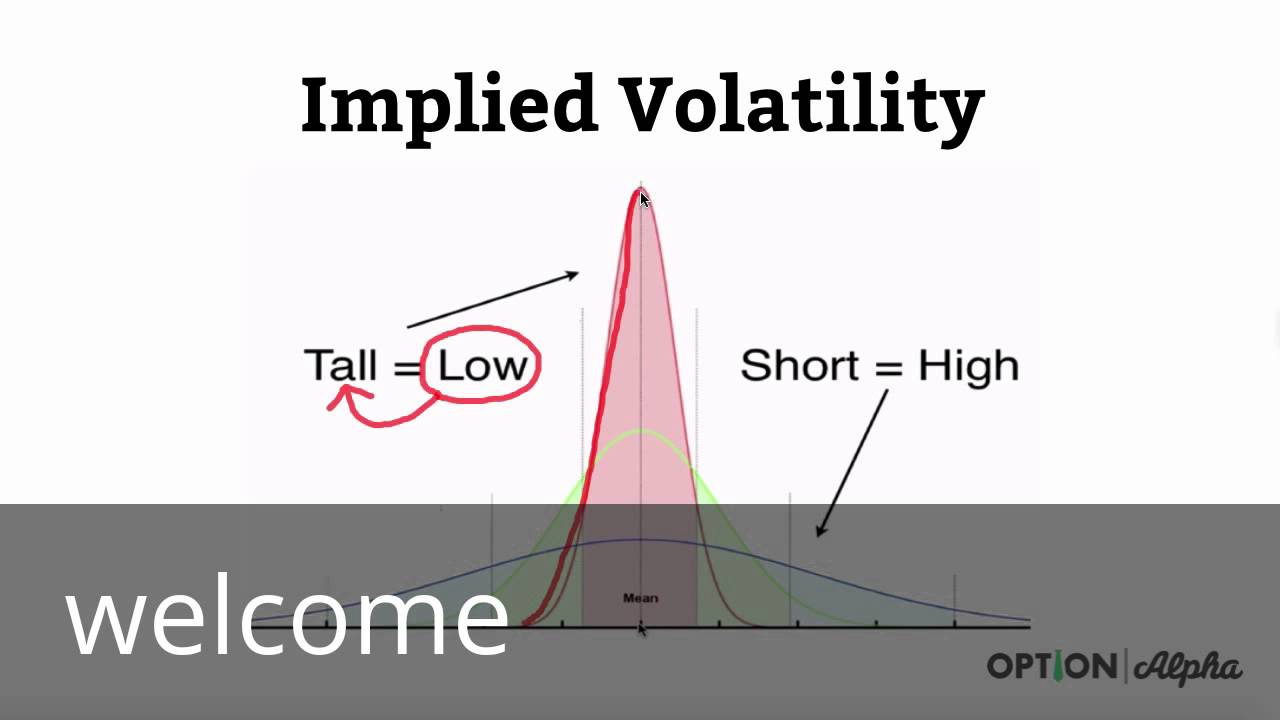
Image: www.youtube.com
At its core, options trading involves the buying and selling of contracts that give the holder the right, but not the obligation, to buy or sell an underlying asset at a specified price on or before a certain date. By understanding the mathematical equations that govern these contracts, traders can make informed decisions about pricing, risk management, and profit potential.
The Black-Scholes Model
The Foundation of Options Pricing
Developed by Fischer Black and Myron Scholes, the Black-Scholes model is a cornerstone of options pricing. This mathematical formula calculates the theoretical fair price of an option based on factors such as the underlying asset’s price, the strike price (the price at which the option can be exercised), the time to expiration, the risk-free interest rate, and the volatility of the underlying asset.
The Black-Scholes model plays a pivotal role in options trading as it provides a benchmark against which traders can assess the reasonableness of option prices and make strategic decisions. By plugging in different values into the equation, traders can determine the fair value of an option and identify potential trading opportunities.
Greeks: Measuring Option Sensitivity
Image: www.mdpi.com
Unlocking Risk Management
Greeks are mathematical measures that quantify the sensitivity of an option’s price to changes in its underlying factors. They provide traders with valuable insights into the risks and potential returns associated with an option position.
The most important Greeks include Delta, Gamma, Theta, Vega, and Rho. Delta measures the change in the option’s price for a unit change in the underlying asset’s price. Gamma measures the change in Delta for a unit change in the underlying asset’s price. Theta measures the change in the option’s price for a unit change in time to expiration. Vega measures the change in the option’s price for a unit change in the volatility of the underlying asset. Rho measures the change in the option’s price for a unit change in the risk-free interest rate.
Implied Volatility: Predicting Future Behavior
Navigating Market Uncertainty
Implied volatility (IV) is a key input in the Black-Scholes model that measures the market’s expectation of future price volatility in the underlying asset. IV is an important indicator for both option buyers and sellers as it affects the pricing and risk of option contracts.
By analyzing historical price data and market sentiment, traders can estimate the implied volatility of an underlying asset to better understand potential price movements and make informed trading decisions.
Tips for Mastering Options Trading Mathematics
Empowering Your Trading Strategy
To effectively master options trading mathematics, traders can follow these expert tips:
- Start with the basics: Begin by understanding the fundamental concepts of option types, strike prices, and expiration dates.
- Practice with a simulator: Use online trading simulators to test your understanding of options trading mathematics in a risk-free environment.
- Seek professional advice: Consult with a financial advisor or experienced options trader to gain guidance and support.
- Stay updated on market trends: Monitor financial news, research reports, and market updates to stay abreast of the latest developments in options trading.
FAQ about Options Trading Mathematics
Here are some commonly asked questions about options trading mathematics:
- Q: What is the Black-Scholes model used for?
A: The Black-Scholes model is used to calculate the theoretical fair price of an option. - Q: What is the difference between Delta and Gamma?
A: Delta measures the sensitivity of an option’s price to changes in the underlying asset’s price, while Gamma measures the sensitivity of Delta to changes in the underlying asset’s price. - Q: What is the significance of implied volatility?
A: Implied volatility indicates the market’s expectation of future price volatility in the underlying asset, influencing the pricing and risk of option contracts. - Q: Can I learn options trading mathematics on my own?
A: With dedication and consistent effort, it is possible to master options trading mathematics through self-study, online resources, and practice.
Options Trading Mathematics
Conclusion
Options trading mathematics is a complex and rewarding discipline that offers traders the potential to enhance their investment strategies. By grasping the fundamental concepts and applying them skillfully, traders can navigate the complexities of options trading and make informed decisions to maximize returns and manage risks effectively. Are you ready to unlock the transformative power of options trading mathematics and unlock new opportunities in the financial markets?






