Have you ever wondered how a seemingly complex concept like option pricing can be distilled into a mathematical formula? Enter the Black-Scholes model, a cornerstone of financial mathematics that revolutionized the way we understand and value options.
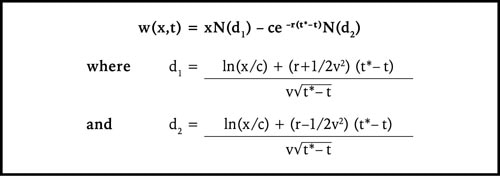
Image: oggsync.com
This guide aims to demystify the intricacies of the Black-Scholes model, presenting it in a clear and accessible manner. Whether you’re a seasoned trader looking to refine your strategies or a curious newcomer eager to understand the world of options, this exploration will equip you with the knowledge to navigate this exciting financial landscape.
The Genesis of Black-Scholes: A Brief History
The Black-Scholes model, developed by economists Myron Scholes and Robert Merton in 1973, emerged as a groundbreaking achievement in financial theory. It was subsequently refined and expanded by Fischer Black, forming the foundational framework used today for pricing options. The model’s significance earned Merton and Scholes the Nobel Memorial Prize in Economic Sciences in 1997 (Black had sadly passed away in 1995).
Prior to the Black-Scholes model, option pricing was largely based on intuition and subjective assessments. The introduction of this mathematical approach brought a new level of objectivity and rigor to the field, enabling traders to make more informed decisions.
The Key Components of the Black-Scholes Formula
The Black-Scholes model, at its core, is a mathematical formula that calculates the theoretical price of a European-style option. The formula takes into account several key factors, including:
- Current Stock Price (S): The current market value of the underlying asset, like a stock, that the option is based on.
- Strike Price (K): The price at which the option holder can buy or sell the underlying asset.
- Time to Maturity (T): The time remaining until the option expires.
- Risk-Free Interest Rate (r): The rate of return on a risk-free investment, like a government bond.
- Volatility (σ): A measure of how much the underlying asset’s price fluctuates.
The formula integrates these variables to determine the “fair value” of an option, representing the price at which the option should trade in a perfectly efficient market.
A Deeper Dive into the Formula’s Implications
Let’s dissect the Black-Scholes formula further to grasp its core concepts:
- Time Value: As time passes, the value of an option decays. This is because the option’s “time premium,” reflecting the uncertainty surrounding the underlying asset’s future price, diminishes. The Black-Scholes formula accounts for this decay.
- Volatility: A higher volatility in the underlying asset’s price leads to a higher option price. This is because there is a greater chance that the asset’s price will move favorably, increasing the potential for profit for the option holder.
- Interest Rates: Higher interest rates generally result in higher option prices, as the discounted value of future cash flows becomes more significant.
Image: math.stackexchange.com
Understanding the Different Types of Options
The Black-Scholes model is primarily used for pricing European-style options, which can only be exercised on the option’s expiration date. However, there are other types of options, including:
- American Options: Can be exercised at any time before expiration, which adds complexity to their pricing model.
- Exotic Options: Have more complex payoff structures and are often priced using numerical methods rather than the Black-Scholes formula.
Practical Applications of the Black-Scholes Model
Beyond theoretical pricing, the Black-Scholes model has a diverse range of practical applications:
- Risk Management: The model helps traders understand and quantify the risk associated with options, enabling them to manage positions effectively.
- Portfolio Optimization: By understanding the price sensitivities of options, investors can optimize their portfolios, incorporating options in a way that aligns with their risk tolerance and financial goals.
- Financial Engineering: The model serves as a foundation for derivative instruments and other complex structured financial products, contributing to broader financial innovation.
Limitations and Considerations of the Black-Scholes Model
While the Black-Scholes model has proven incredibly valuable, it’s not without its limitations:
- Assumptions: The model relies on several idealized assumptions, such as constant volatility and risk-free interest rates, which may not hold true in real-world markets.
- Market Efficiency: The model assumes that markets are perfectly efficient, with no frictions or imperfections. In reality, market dynamics are often influenced by factors like liquidity and information asymmetry.
- Volatility Estimation: Estimating volatility accurately is crucial for the model’s effectiveness. However, volatility can be unpredictable, and historical data may not always provide a reliable forecast.
Despite these limitations, the Black-Scholes model remains a powerful tool for analyzing and pricing options. It is crucial to consider its assumptions and limitations, and to use it in conjunction with other analytical tools and market insights.
Black-Scholes in Action: A Real-World Example
Imagine you’re considering buying a call option on ABC stock, with a strike price of $100 and a maturity of 6 months. The current stock price is $95, the risk-free interest rate is 2%, and the volatility is estimated at 20%. By plugging these values into the Black-Scholes formula, you would obtain the theoretical price of the call option. This price can then be compared to the market price to gauge whether the option is undervalued or overvalued.
By comparing the theoretical price to the market price, you can make an informed decision on whether to buy or sell the option. This process highlights how the Black-Scholes model can provide quantitative insights into option valuation, assisting traders in making informed decisions.
Beyond the Basics: Advanced Techniques and Extensions
While the basic Black-Scholes model serves as a solid foundation, there are several extensions and advanced techniques that address its limitations and broaden its applicability:
- The Binomial Tree Model: This method approximates the underlying asset’s price movement using discrete steps, offering an alternative to the continuous model used in Black-Scholes.
- Monte Carlo Simulation: This technique relies on generating random price paths for the underlying asset to simulate the option’s payoff over time.
- Implied Volatility: Instead of assuming a fixed volatility, this approach uses market prices to extract “implied volatility” – a measure of the market’s expectation of future volatility.
These techniques provide greater flexibility and adaptability in addressing specific market conditions and option types, allowing for a more nuanced approach to option pricing and risk management.
Basic Black-Scholes Option Pricing And Trading Pdf
Conclusion: Your Journey in Options Pricing
The Black-Scholes model has undeniably revolutionized option pricing, providing a rigorous framework for understanding these complex financial instruments. While it has its limitations, its applications in risk management, portfolio optimization, and financial engineering are undeniable. By understanding the model’s core concepts and its strengths and weaknesses, you gain a valuable advantage in navigating the world of options.
We encourage you to explore further resources, including academic texts and online tutorials, to deepen your knowledge of option pricing, risk management, and hedging strategies. The journey of understanding options is both intellectually stimulating and practically rewarding. As you explore the world of options, remember that the Black-Scholes model is a vital tool in your arsenal, empowering you to make informed decisions and navigate the dynamic world of finance.






