Unveiling the Mathematical Underpinnings of Options Pricing
In the realm of finance, options have emerged as versatile financial instruments that empower traders with unparalleled flexibility in managing risk and seeking profit. However, mastering the intricacies of options pricing requires a deep understanding of the underlying mathematical framework known as the calculus of options trading. This article delves into the theoretical foundations and practical applications of this vital tool, enabling traders to enhance their decision-making and optimize their trading strategies.
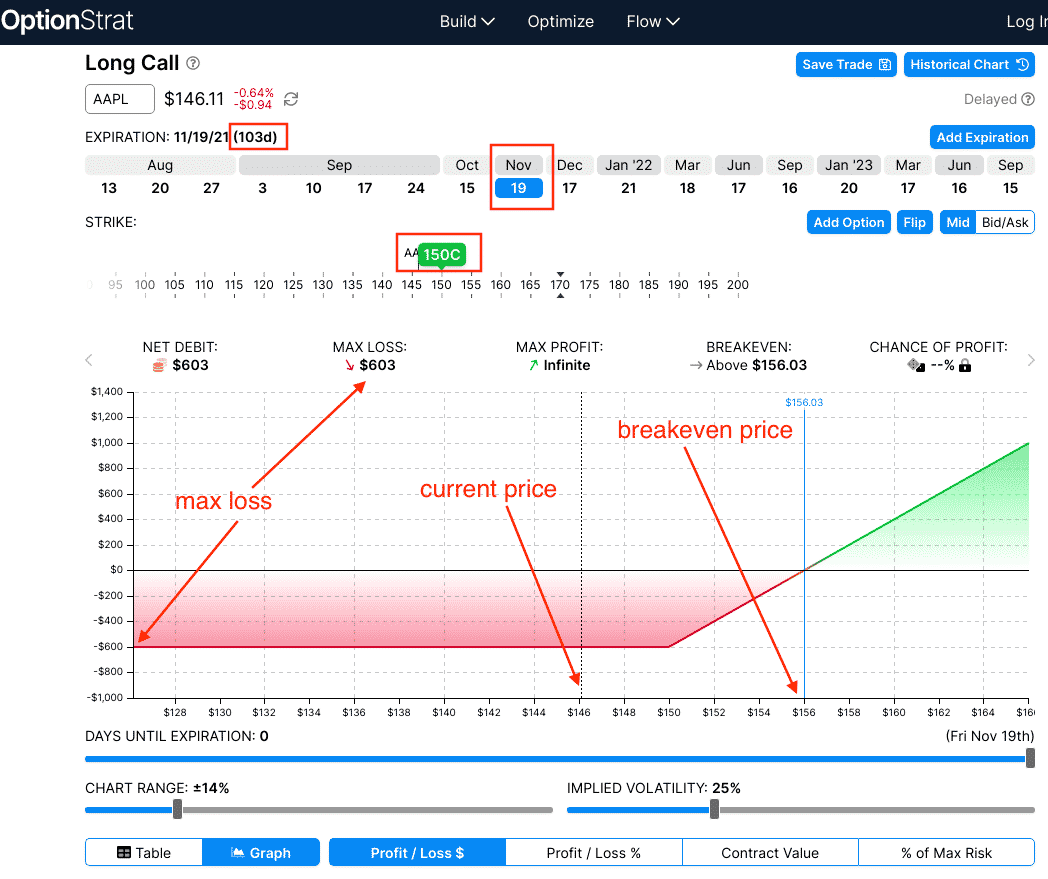
Image: optionstradingiq.com
Understanding the Greeks: Deciphering Option Sensitivities
At the heart of the calculus of options trading lies a group of metrics known as the Greeks. These sensitivity measures quantify the impact of various factors on an option’s price, providing traders with crucial insights into market dynamics. Delta, Gamma, Theta, Vega, and Rho are prominent members of the Greek alphabet that bear significance in options trading. Understanding these measures and their interplay empowers traders to make informed adjustments to their trading positions in response to market shifts.
Black-Scholes Model: Groundwork of Option Valuation
Among the array of option pricing models, the Black-Scholes model stands as a cornerstone of options trading. Developed by Fischer Black and Myron Scholes in the 1970s, this model provides a mathematical framework for valuing options based on underlying asset price, strike price, time to expiration, risk-free interest rate, and volatility. The Black-Scholes formula has become an industry standard, offering traders a reliable tool for assessing option prices and gauging market sentiment.
Hedging Strategies: Mitigating Risk through Options
The calculus of options trading also plays a pivotal role in formulating effective hedging strategies. Hedging involves using options to reduce the risk associated with an underlying asset or portfolio. By understanding the sensitivity measures and option pricing models, traders can construct tailored hedges that neutralize or reduce market-induced losses. Hedging empowers investors to manage risk and secure downside protection, ensuring greater peace of mind in turbulent markets.

Image: www.cnblogs.com
Binomial and Monte Carlo Models: Capturing Market Dynamics
The Black-Scholes model, while widely employed, has inherent limitations, such as its inability to account for path-dependent options or discontinuous dividend payments. In such scenarios, traders turn to more sophisticated models, such as the binomial and Monte Carlo models. Binomial trees provide a discrete approach to option pricing, while Monte Carlo simulations leverage random sampling to approximate complex non-linear dynamics of the underlying asset. These advanced techniques provide greater accuracy in option valuation and cater to a broader range of trading scenarios.
The Calculus Of Options Trading
Image: comparesharebrokers.com
Conclusion
The calculus of options trading serves as a powerful tool, offering traders a comprehensive understanding of option pricing and its sensitivity to market fluctuations. From the fundamental Greeks to complex pricing models like Black-Scholes, binomial trees, and Monte Carlo simulations, this mathematical framework empowers traders to make informed decisions, manage risk, and optimize their trading strategies. By mastering the calculus of options trading, traders unlock a wealth of insights into the dynamics of this multifaceted financial instrument, paving the way for enhanced profitability and success in the ever-evolving options market.






