Introduction
In the realm of options trading, understanding Graham convexity is crucial for strategic decision-making. As an options enthusiast, I recently encountered an intriguing scenario that vividly illustrated the significance of Graham convexity. I ventured into a deep analysis of this concept, unlocking a treasure trove of insights. Now, I’m eager to share my knowledge and guide you through the intricacies of Graham convexity.
Image: publications.banque-france.fr
Unveiling Graham Convexity
Graham convexity refers to the nonlinear relationship between an option’s price and its underlying asset’s price. As the underlying asset price fluctuates, the rate of change in the option’s price exhibits a curved trajectory. This curvature is graphically represented by the “Graham’s hook,” showcasing the nonlinearity inherent in option pricing.
The Significance of Volatility
Volatility plays a pivotal role in shaping Graham convexity. Higher volatility translates into a steeper Graham’s hook, indicating a more pronounced curvature in the option’s price movement. This emphasizes the influence of volatility in amplifying the sensitivity of option prices to changes in the underlying asset’s price.
Exploring Positive and Negative Graham Convexity
Graham convexity assumes two forms: positive and negative. Positive Graham convexity characterizes options that have a convex upward curvature, meaning their prices rise at a faster rate than the underlying asset. Conversely, negative Graham convexity depicts options with a convex downward curvature, signifying a slower rise in their prices compared to the underlying asset.
Image: tonyhieu.github.io
Analyzing the Benefits of Graham Convexity
Harnessing Graham convexity can empower options traders with numerous advantages:
- Enhanced profit potential: Options with positive Graham convexity offer the potential for heightened profits, particularly in volatile market conditions where the underlying asset experiences significant price swings.
- Hedging volatility: By strategically incorporating options with positive Graham convexity into hedging strategies, traders can mitigate the impact of asset price volatility.
Navigating the Risks Associated with Graham Convexity
Despite its benefits, Graham convexity also poses certain risks:
- Limited profit potential: Options with negative Graham convexity may restrict profit potential, especially in scenarios where the underlying asset price remains relatively stable.
- Increased loss risk: In volatile markets, options with negative Graham convexity can amplify losses, amplifying the financial impact of adverse price movements.
Expert Insights and Practical Tips
Mastering Graham convexity demands a comprehensive understanding of its nuances. Here are some expert tips to guide your decision-making:
- Identify appropriate time frames: The impact of Graham convexity varies with time to expiration. Options with longer time frames tend to exhibit more pronounced convexity effects.
- Factor in volatility expectations: Volatility expectations greatly influence the shape of Graham’s hook. Adjusting strategies based on volatility forecasts enhances the efficacy of convexity trading.
- Utilize specialized tools: Quantifying and analyzing Graham convexity requires specialized tools, such as pricing models and calculators. These tools facilitate accurate assessment and informed decision-making.
FAQ on Graham Convexity
Q: How can I determine if an option has positive or negative Graham convexity?
A: Examining the relationship between the option’s price and the underlying asset’s price provides insight into convexity. Positive Graham convexity is characterized by a faster rate of increase in the option’s price compared to the underlying asset, while negative Graham convexity manifests as a slower rate of increase.
Q: In which scenarios is Graham convexity particularly advantageous?
A: Graham convexity offers significant advantages in volatile markets. When the underlying asset price experiences large swings, options with positive Graham convexity possess the potential to generate substantial profit.
Graham Convexity Option Trading
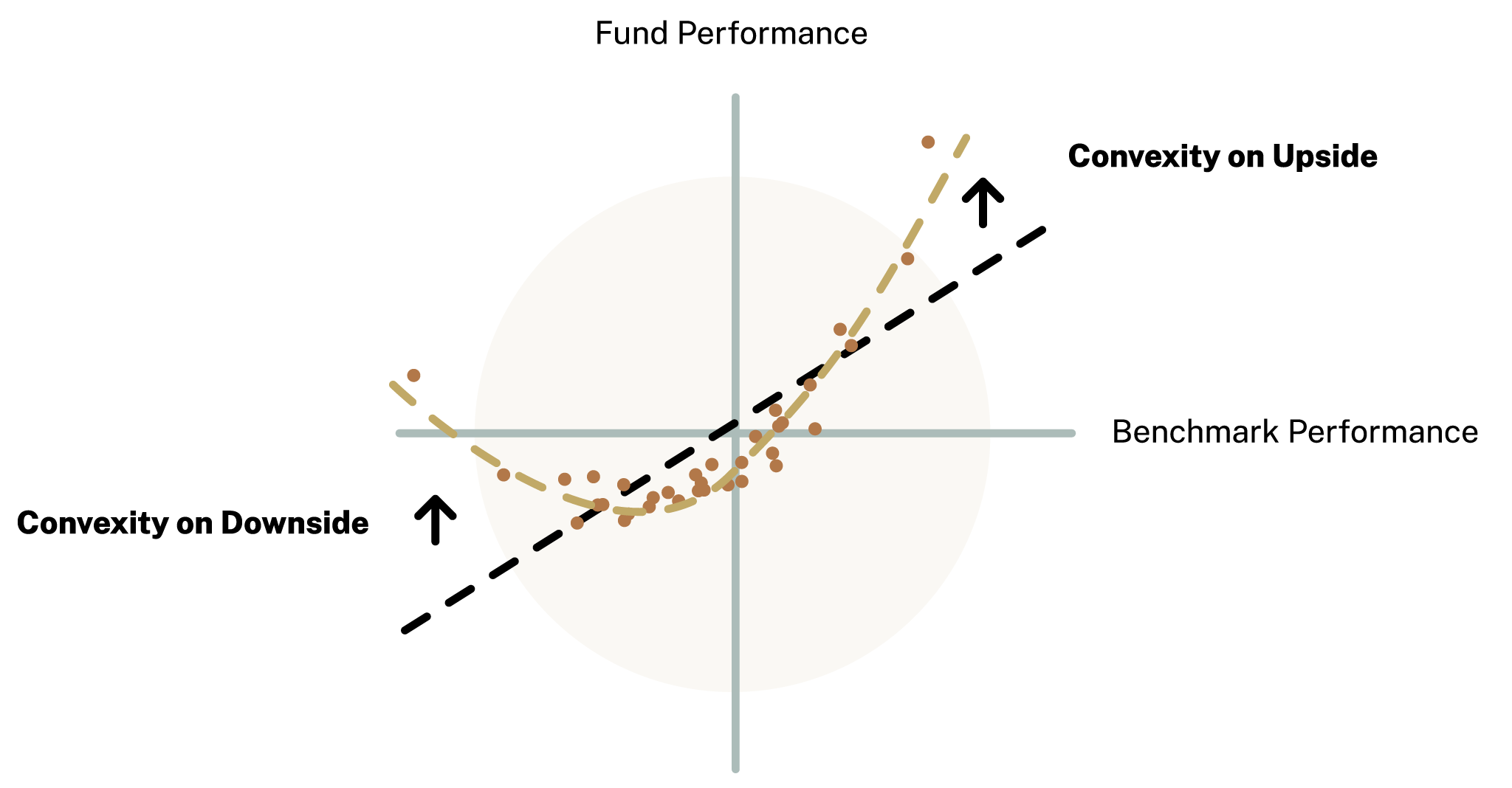
Image: seekingalpha.com
Conclusion
Graham convexity is an indispensable concept in options trading, allowing traders to capitalize on the nonlinear relationship between option prices and underlying asset prices. By leveraging expert insights, practical tips, and a deep understanding of Graham convexity, traders can navigate complex market conditions, optimize profit potential, and mitigate potential risks. As you continue your exploration of the intricate world of Graham convexity, I encourage you to delve deeper into its applications, continuously hone your knowledge, and engage with fellow traders to exchange invaluable experiences and perspectives. Are you ready to unlock the transformative power of Graham convexity in your option trading strategies?






